Lie bracket of vector fields

See Lie algebra for more on the definition of the Lie bracket and Lie derivative for the derivation

In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]. It is the specialization of the Lie derivative to the case of Lie differentiation of a vector field. 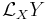Indeed, [X,Y] equals the Lie derivative \mathcal{L}_X Y.

It plays an important role in differential geometry and differential topology, and is also fundamental in the geometric theory for nonlinear control systems (Isaiah 2009, pp. 20–21, nonholonomic systems; Khalil 2002, pp. 523–530, feedback linearization).

A generalization of the Lie bracket (to vector-valued differential forms) is the Frölicher–Nijenhuis bracket.

Contents

Definition

Each vector field X on a smooth manifold M may be regarded as a differential operator acting on smooth functions on M. Indeed, for each p, the vector X(p) is a derivation on the smooth functions defined near p. The Jacobi–Lie bracket or simply Lie bracket, [X,Y], of two vector fields X and Y is the differential operator defined by

[X,Y](f)�:= X(Y(f))-Y(X(f)) \,.

One can show that, at each point, this operator is a derivation, and hence the Lie bracket is a vector field.

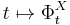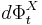To make the connection to the Lie derivative, let t \mapsto \Phi^X_t be the 1-parameter group of diffeomorphisms (or flow) generated by the vector field X . The differential d\Phi^X_t of each diffeomorphism maps the vector field Y to a new vector field 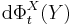\mathrm{d}\Phi^X_{t}(Y). To pull-back the vector field one applies the differential of the inverse, 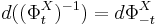d ((\Phi^X_{t})^{-1})= d \Phi_{-t}^X . The Lie bracket is defined by

[X, Y]_x�:= \lim_{t \to 0}\frac{(\mathrm{d}\Phi^X_{-t}) Y_{\Phi^X_t(x)} - Y_x}t = \left.\frac{\mathrm{d}}{\mathrm{d} t}\right|_{t=0} (\mathrm{d}\Phi^X_{-t}) Y_{\Phi^X_t(x)}

In particular, [X,Y] is the Lie derivative of the vector field Y with respect to X. Conceptually, the Lie bracket is the derivative of Y in the `direction' generated by X .

Though neither definition of the Lie bracket depends on a choice of coordinates, in practice one often wants to compute the bracket with respect to a coordinate system. Let 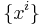\{x^i \} be a set of local coordinate functions, and let 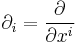\partial_i = \frac{\partial}{\partial x^i} denote the associated local frame. Then

[X,Y]�:= (X(Y^i) - Y(X^i)) \partial_i = \left(X^j \partial_j Y^i - Y^j \partial_j X^i \right) \partial_i

(Here we use the Einstein summation convention)

Properties

The Lie bracket of vector fields equips the real vector space 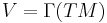V=\Gamma(TM) (i.e., smooth sections of the tangent bundle of M) with the structure of a Lie algebra, i.e., [·,·] is a map from 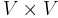V\times V to V with the following properties

[fX, gY] = fg [X,Y] %2B fX(g) Y - gY(f) X.

These three properties together also define a Lie algebroid. Note that the infinite dimensional Lie algebra has nice topological properties.

An immediate consequence of the second property is that [X,X]=0 for any X.

The name commutator is used because the Lie bracket is the commutator of the vector fields considered as differentiable operators. We also have the following fact:

Theorem:

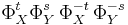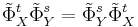[X,Y]=0\, iff the commutator of flows \Phi_X^t \Phi_Y^s\,\Phi_X^{-t}\, \Phi_Y^{-s} is a closed loop. Alternatively the lift of the flows on the universal covering commute \tilde\Phi_X^t\tilde \Phi_Y^s = \tilde\Phi_Y^s\tilde\Phi_X^t\,.

Examples

For a Lie group, the Lie algebra is tangent space at the identity, which can be identified with the left invariant vector fields. The Lie bracket of the Lie algebra is then the Lie bracket of the left invariant vector fields, which is also left invariant.

For a matrix Lie group, smooth vector fields can be locally represented in the corresponding Lie algebra. Since the Lie algebra associated with a Lie group is isomorphic to the group's tangent space at the identity, elements of the Lie algebra of a matrix Lie group are also matrices. Hence the Jacobi–Lie bracket corresponds to the usual commutator for a matrix group:

[X,Y] = XY - YX

where juxtaposition indicates matrix multiplication.

Applications

The Jacobi–Lie bracket is essential to proving small-time local controllability (STLC) for driftless affine control systems.

References